Safe Haskell	Safe
Language	Haskell98

Data.Nested.Seq.Binary.Lazy

Contents

Accessing the left end of the sequence
Basic queries
Basic construction
Short sequences
Unsafe head and tail
Safe head and tail
Indexing
Slow operations
Debugging

Description

Simple but efficient lazy list-like sequence type based on a nested data type and polymorphic recursion. Also called "binary random-access list"

It is like a list, but instead of O(1) cons/uncons and O(k) lookup, we have amortized O(1) cons/uncons and O(log(k)) lookup (both are O(log(n)) in the worst case). This is somewhat similar to a finger tree (which is also represented by a nested data type), but much simpler. Memory usage is basically the same as with lists: on average 3 words per element, plus the data itself.

However, modifying the right end of the sequence is still slow: O(n). This affects the functions snoc, unSnoc, append, take, init. Somewhat surprisingly, extracting the last element is still fast.

An example usage is a stack.

This module is intended to be imported qualified.

Synopsis

Documentation

data Seq a Source #

The lazy sequence type.

The underlying (nested) data structure corresponds to the binary representation of the length of the list. It looks like this:

data Seq a
  = Nil
  | Even   (Seq (a,a))
  | Odd  a (Seq (a,a))

Furthermore we maintain the invariant that Even Nil never appears.

If the Odd constructor was missing, this would be a full binary tree. Note that the nested data type representation has two advantages compared to a naive binary tree type (by which we mean the usual data Tree a = Node a a | Leaf a construction): First, the type system guarantees the fullness; second, it has smaller memory footprint, since in the naive case, the Leaf constructors introduce two extra words (a tag word and a pointer).

With the Odd constructor thrown in, this is a sequence of larger and larger full binary trees. Looking at the binary representation of the length of the list, we will have full binary trees corresponding to the positions of 1 digits.

For example, here are how sequences of lengths 4, 5, 6 and 7 are represented:

Instances

Functor Seq #
Methods fmap :: (a -> b) -> Seq a -> Seq b # (<$) :: a -> Seq b -> Seq a #
Foldable Seq #
Methods fold :: Monoid m => Seq m -> m # foldMap :: Monoid m => (a -> m) -> Seq a -> m # foldr :: (a -> b -> b) -> b -> Seq a -> b # foldr' :: (a -> b -> b) -> b -> Seq a -> b # foldl :: (b -> a -> b) -> b -> Seq a -> b # foldl' :: (b -> a -> b) -> b -> Seq a -> b # foldr1 :: (a -> a -> a) -> Seq a -> a # foldl1 :: (a -> a -> a) -> Seq a -> a # toList :: Seq a -> [a] # null :: Seq a -> Bool # length :: Seq a -> Int # elem :: Eq a => a -> Seq a -> Bool # maximum :: Ord a => Seq a -> a # minimum :: Ord a => Seq a -> a # sum :: Num a => Seq a -> a # product :: Num a => Seq a -> a #
Eq a => Eq (Seq a) #
Methods (==) :: Seq a -> Seq a -> Bool # (/=) :: Seq a -> Seq a -> Bool #
Ord a => Ord (Seq a) #
Methods compare :: Seq a -> Seq a -> Ordering # (<) :: Seq a -> Seq a -> Bool # (<=) :: Seq a -> Seq a -> Bool # (>) :: Seq a -> Seq a -> Bool # (>=) :: Seq a -> Seq a -> Bool # max :: Seq a -> Seq a -> Seq a # min :: Seq a -> Seq a -> Seq a #
Show a => Show (Seq a) #
Methods showsPrec :: Int -> Seq a -> ShowS # show :: Seq a -> String # showList :: [Seq a] -> ShowS #
Monoid (Seq a) #
Methods mempty :: Seq a # mappend :: Seq a -> Seq a -> Seq a # mconcat :: [Seq a] -> Seq a #

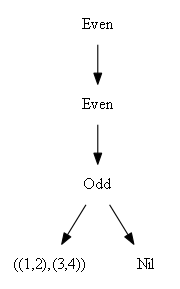
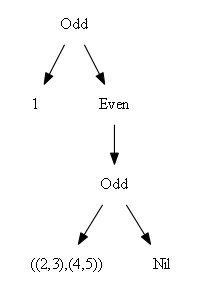
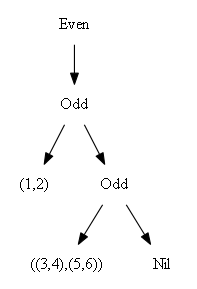
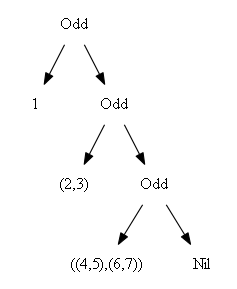
Accessing the left end of the sequence

cons :: a -> Seq a -> Seq a Source #

Prepending an element. Worst case O(log(n)), but amortized O(1).

unCons :: Seq a -> Maybe (a, Seq a) Source #

Worst case O(log(n)), amortized O(1)

Basic queries

null :: Seq a -> Bool Source #

Checks whether the sequence is empty. This is O(1).

length :: Seq a -> Int Source #

The length of a sequence. O(log(n)).

Basic construction

empty :: Seq a Source #

The empty sequence.

toList :: Seq a -> [a] Source #

Conversion to a list. O(n).

fromList :: [a] -> Seq a Source #

Conversion from a list. O(n).

Short sequences

singleton :: a -> Seq a Source #

pair :: a -> a -> Seq a Source #

triple :: a -> a -> a -> Seq a Source #

quad :: a -> a -> a -> a -> Seq a Source #

Unsafe head and tail

head :: Seq a -> a Source #

First element of the sequence. Worst case O(log(n)), amortized O(1).

tail :: Seq a -> Seq a Source #

Tail of the sequence. Worst case O(log(n)), amortized O(1).

last :: Seq a -> a Source #

Last element of the sequence. O(log(n)).

Safe head and tail

mbHead :: Seq a -> Maybe a Source #

First element of the sequence. Worst case O(log(n)), amortized O(1).

mbTail :: Seq a -> Maybe (Seq a) Source #

Tail of the sequence. Worst case O(log(n)), amortized O(1).

tails :: Seq a -> [Seq a] Source #

All tails of the sequence (starting with the sequence itself)

mbLast :: Seq a -> Maybe a Source #

Last element of the sequence. O(log(n))

Indexing

lookup :: Int -> Seq a -> a Source #

Lookup the k-th element of a sequence. This is worst case O(log(n)) and amortized O(log(k)), and quite efficient.

mbLookup :: Int -> Seq a -> Maybe a Source #

update :: (a -> a) -> Int -> Seq a -> Seq a Source #

Update the k-th element of a sequence.

replace :: Int -> a -> Seq a -> Seq a Source #

Replace the k-th element. replace n x == update (const x) n

drop :: Int -> Seq a -> Seq a Source #

Drop is efficient: drop k is amortized O(log(k)), worst case maybe O(log(n)^2) ?

Slow operations

append :: Seq a -> Seq a -> Seq a Source #

O(n) (for large n at least), where n is the length of the first sequence.

take :: Int -> Seq a -> Seq a Source #

Take is slow: O(n)

init :: Seq a -> Seq a Source #

The sequence without the last element. Warning, this is slow, O(n)

mbInit :: Seq a -> Maybe (Seq a) Source #

The sequence without the last element. Warning, this is slow, O(n)

snoc :: Seq a -> a -> Seq a Source #

Warning, this is slow: O(n) (with bad constant factor).

unSnoc :: Seq a -> Maybe (Seq a, a) Source #

Stripping the last element from a sequence is a slow operation, O(n). If you only need extracting the last element, use mbLast instead, which is fast.

Debugging

toListNaive :: Seq a -> [a] Source #

Naive implementation of toList

checkInvariant :: Seq a -> Bool Source #

We maintain the invariant that (Z Nil) never appears. This function checks whether this is satisfied. Used only for testing.

showInternal :: Show a => Seq a -> String Source #

Show the internal structure of the sequence. The constructor names Z and O come from "zero" and "one", respectively.

graphviz :: Show a => Seq a -> String Source #

Generates a graphviz DOT file, showing the internal structure of a sequence